Distributing Extra Space in an EW-Array

An EW-Array employs all three of the above techniques. A large $D_d$ value allows for more efficient writes. A large $D_s$ value more aggressively reduces the seek cost. A large $D_m$ value more aggressively reduces the rotational cost of reads. Given a total budget of $D$ disks and the constraint $D = D_d \times D_m \times D_s$, one must carefully balance these three dimensions to optimize the overall performance. The decision of how to configure these three dimensions is influenced by both the workload and disk characteristics. A workload that has a small read-to-write ratio and little idle time demands a large dilution factor $D_d$ so that more resources are devoted to speeding up writes. Disks with large seek delays demand a large striping factor $D_s$, while disks with large rotational delay demand a large mirroring factor $D_m$.

In this section, we explore the impact of array configurations using a simple synthetic workload (that is part of the Intel ``Iometer'' benchmark [15]). More complex workloads are explored in Section 6. In each of the test runs, the length of the queue of the outstanding requests is kept at a constant. This is accomplished by adding a new request to the queue as soon as an old one is retired from it. Different queue lengths emulate different degree of idleness in the system. In all runs, the read/write ratio is 50/50.

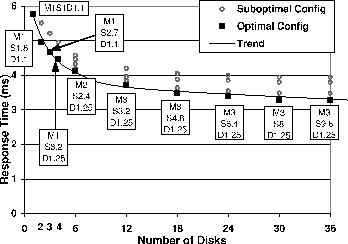
Figure 2 compares the latency of alternative EW-Array configurations. In these experiments, the number of outstanding requests is one so there is no queueing. As a result, a relatively small dilution factor ($D_d=1.25$) is generally sufficient for absorbing the writes while a relatively large $D_m \times D_s$ product improves read latency. A properly configured 4-disk EW-Array halves the latency achieved on a single-disk conventional system. Note that many of the configurations in Figure 2 have fractional values for $D_s$ and $D_d$, yet $D_s \times D_d$ is always integral. That means each replica stripes data across $D_s \times D_d$ disks. On each of those disks, only $1/D_s$ fraction of the tracks are actually used to store data, and utilization of those tracks is $1/D_d$.

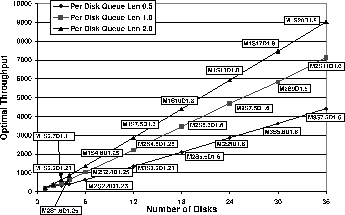
Figure 3 shows how the throughput of optimally configured EW-Arrays scales with an increasing number of disks. We vary the number of outstanding requests per disk to emulate different load levels. For a fixed number of disks, as we raise the request arrival rate, a progressively larger dilution factor $D_d$ is needed to absorb the disk writes that can no longer be masked by idle periods.

Figure 2: Comparison of response times of different EW-Array configurations. Each point symbol shows the performance of an alternative EW-Array configuration. A label ``MaSbDc'' denotes a $D_m \times D_s \times D_d = a \times b \times c$ configuration.

Figure 3: Throughput of optimal EW-Array configurations under different queueing conditions. Each point represents the performance of an EW-Array configuration.