Communication Granularity

Communication granularity plays an important role in shaping the bottom line performance. They also stress different aspects of the underlying hardware. Consider the following code fragments:

    A () {                               B () {                  
                                             repeat 1M times {
        read 1 MB;                               read 1 B;       
        compute on this 1 MB;                    compute on this 1 B; 
                                             }
    }                                    }

Function A stresses bandwidth while function B is sensitive to latency. A high per message overhead is likely to cost B dearly while A has the potential of amortizing it. Yet these two functions have identical traffic to instruction ratio. As an example, the following figure shows the obvious performance benefit of the bulk operations.

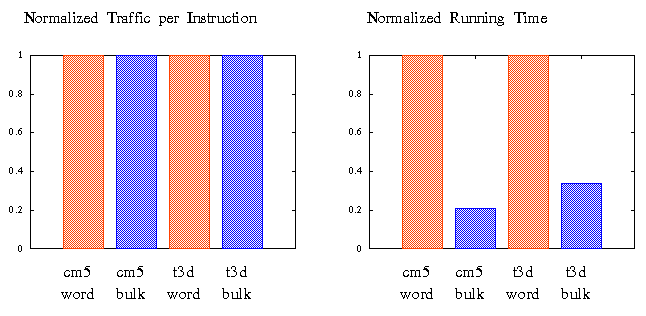
Fundamentally, what this metric has hidden is the ability to overlap communication with communication. It also hides the peak bandwidth demand under the facade of an average. A more meaningful measure should break this average down into a histogram so we have a more precise idea about how much communication is required before each computation.

The issue of communication granularity becomes even more relevant when we start to explore different coherence models. For example, the SAM??? object layer provides coherence at the granularity of objects instead of cache lines. Programs can be manipulating objects at drastically different granularities with drastically different costs, and yet share the same communication per instruction metric.